Determine the Value of a and B That Make F X Continuous

Find values of $a$ and $b$ that make the function continuous everywhere.

Solution 1

I've seen this problem before and it looks like this may be the function you are trying to make continuous here:

$f(x) = \begin{cases} \frac{x^2-4}{x-2} & \mbox{if } x<2 \\ ax^2-bx+1 & \mbox{if } 2\leq x<3 \\ 4x-a+b & \mbox{if } x\geq 3 \end{cases}$

To make sure $f$ is continuous at $x=2$ you want to use the definition of what it means to be continuous by solving $\lim_{x \to 2} f(x) = f(2).$ Since $f$ is different from the left and right side of $x=2$, you need to instead find each one sided limit.

$$\lim_{x \to 2^{-}} f(x) = f(2)$$

$$\lim_{x \to 2^{+}} f(x) = f(2).$$

First the left sided limit: $$\lim_{x \to 2^{-}} \frac{x^2-4}{x-2} = f(2)$$ $$\lim_{x \to 2^{-}} \frac{(x+2)(x-2)}{x-2} = f(2)$$ $$\lim_{x \to 2^{-}} (x+2) = f(2)$$ $$4=f(2)$$ $$4=a(2)^2-b(2)+1$$ $$4=4a-2b+1$$ $$3=4a-2b$$ If you do this with the right sided limit, you'll see that you end up with $4a-2b+1=4a-2b+1$, which doesn't really give you any useful information. Now you want to do the same thing to make sure $f$ is continuous at $x=3$ $$\lim_{x \to 3^{-}} f(x) = f(3)$$ $$\lim_{x \to 3^{-}} ax^2-bx+1 = 12-a+b$$ $$a(3)^2-b(3)+1 = 12-a+b$$ $$9a-3b+1 = 12-a+b$$ $$10a-4b=11$$

And in this case, the right sided limit won't contribute anything useful. Now you just need to solve the following system of equations:

$$3=4a-2b$$ $$10a-4b=11$$

Here's a link to a very detailed work-through of a very similar problem with a bit more explanation of why this works.

https://jakesmathlessons.com/limits/solution-find-the-values-of-a-and-b-that-make-f-continuous-everywhere/

Solution 2

If $f$ is continuous then :

$f(2)=\underset{x\rightarrow2}{\lim}f(x)=2^2-\frac{4}2-2=a(2^2)-b(2)+1$

Therefore $4a-2b+1=4-2-2=0$ hence $4a-2b+1=0$.

Same reasoning around $x=3$ :

$a(3^2)-b(3)+1=4(3)-a+b$ (ie) $9a+3b+1=12-a+b$ therefore $10a-4b=11$

You just need to solve $\begin{cases}4a-2b=-1\\10a-4b=11\end{cases}$ to find $a$ and $b$.

Solution 3

For continuity at 2, we need $\lim_{x\to2^{+}}f(x)=f(2)$ and $\lim_{x\to2^{-}}f(x)=f(2)$, so $4a-2b+1=4a-2b+1$ and $4-2-2=4a-2b+1$, so $4a-2b=-1$.

For continuity at 3, we need $\lim_{x\to3^{+}}f(x)=f(3)$ and $\lim_{x\to3^{-}}f(x)=f(3)$, so $12-a+b=9a-3b+1$ and $9a-3b+1=9a-3b+1$, so $10a-4b=11$.

Now solve these two equations for a and b.

(I am assuming the last part of the definition should say for $x>3$.)

Comments

I need some help with this question:

Find the values of $a$ and $b$ that make $f$ continuous everywhere.

$$f(x)=\begin{cases} x^2 − 4/x-2, &\text{if }x < 2\\ ax^2-bx+1, &\text{if } 2 ≤ x ≤ 3\\ 4x - a + b, &\text{if } x ≥ 3\end{cases}$$

I started by writing two expressions for $a$ and $b$ based upon the left and right limits of each piece's endpoints. But I ended up with $a=3/2$ and $b=2/3$. Where did I go wrong?
- What equations did you get for a and b after you found the one-sided limits?
- All I did was plug in numbers into the equation at x = 2 (for x^2-4/x-2 and ax^2-bx+1) and then x = 3 (ax^2-bx+3 and 4x-a+b)
- @Michael are you sure it's $4/x$ and not $4x$ for the part where $x<2$ ?
- Maybe the first option was meant to evaluate to $(x^2-4)/(x-2)$? The original was somewhat unclear on this matter. (Also, both the second and third options seem to apply when $x=3$, which won't change the answer, but you should probably check if the second option is meant to hold when $... x < 3$ or the third option when $x > 3$.)
so A = 7/5 and B = -33/10?
Ugh! It didn't like either of those answers I wrote...
@Michael Maybe $a=2,b=\frac{-9}2$ ?
Nope, that's not the answer either...
@Michael What is it supposed to be ?
No idea... It doesn't show the answer...
@Michael Here fixed
@Michael $a=13/2,b=27/2$ ?
Mmmm Still incorrect... I think B is supposed to cancel out...
@Michael Can you link me to the source ? Both answers that have been posted here give the $a,b$ I just posted above, so ...
I'm afraid there isn't a source... I ran out of attempts anyways... It still didn't show me the correct answer...
It was just a homework question on a math assignment...
@Michael Look at this prntscr.com/4lxjou to me it IS continuous (I drew it in red). Maybe the form you answered on didn't support fractions, or something like that.

Recents

What is the matrix and directed graph corresponding to the relation $\{(1, 1), (2, 2), (3, 3), (4, 4), (4, 3), (4, 1), (3, 2), (3, 1)\}$?

bastienhavine.blogspot.com

Source: https://9to5science.com/find-values-of-a-and-b-that-make-the-function-continuous-everywhere

Determine the Value of a and B That Make F X Continuous

Find values of $a$ and $b$ that make the function continuous everywhere.

Solution 1

Solution 2

Solution 3

Related videos on Youtube

Comments

Recents

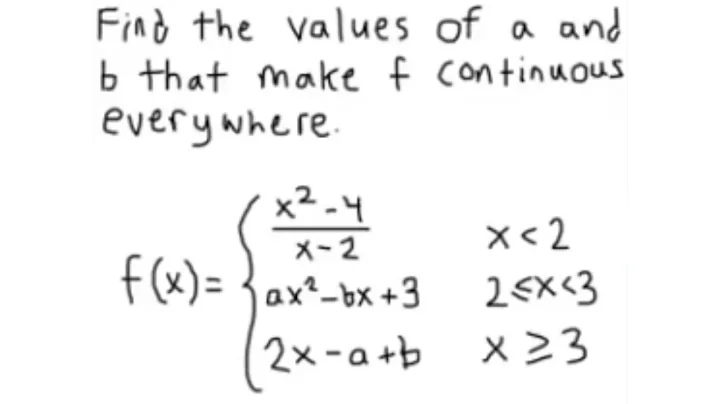
0 Response to "Determine the Value of a and B That Make F X Continuous"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel